Помогите узнать площадь — и прочие школьные задачки
ИмхоДом › Форумы › свободная тема › Помогите узнать площадь — и прочие школьные задачки
- В этой теме 66 ответов, 32 участника, последнее обновление ⤠ сделано
 День за днем.
День за днем.
-
АвторСообщения
-
25 Июл'14 в 03:24 #7746
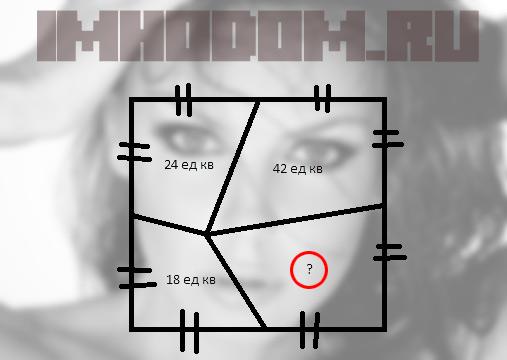
вот эта задачка оказывается вполне решаема. Сколько единиц площади в вопросительном знаке?
25 Июл'14 в 03:27 #103305Больше 24, но меньше 42 ))
25 Июл'14 в 03:32 #103306почти наугад — 28
25 Июл'14 в 03:57 #10330836
25 Июл'14 в 04:02 #10330937 и длина стороны 11
25 Июл'14 в 04:08 #103310чо-то вообще не соображу, с какого боку подступиться…
25 Июл'14 в 04:17 #103311Эхх.. Пропал рабочий день..
25 Июл'14 в 04:23 #103312Ура рабочий день спасен! Общая площадь 120 ед.кв. Сторона квадрата 10,95 ед., Неизвестная площадь 36 ед.кв.
25 Июл'14 в 04:34 #103313но как? каков ход мысли?
25 Июл'14 в 04:41 #103314Два листа исписал, всякие там системы уравнений составляя))) всякая ерунда получается!
Короче это только предположение: сумма площадей располагаемых по диагонали равна половине площади всего квадрата. Тогда 42+18=60, а площадь всего квадрата 120, а недостающая площадь 120-84=36.
25 Июл'14 в 06:45 #10331631,5 м2, 115,5 м2 и 10,75 м..
25 Июл'14 в 06:51 #103317Ну прям интрига! Ждемс правильного ответа)))
25 Июл'14 в 07:09 #103318Ответ действительно 36.
Общая площадь 120 (нужно ещё доказать что противоположенные площади будут равны),
мой ход мыслей: выражаем высоты опущенные из точки на стороны вписанного квадрата через площади известные. в итоге получаем что треугольникв неизвестной области будет равен 36-а^2, а так как прямоугольный треугольник в неизвестной области по сторонам исходного квадрата равен а^2…
25 Июл'14 в 07:49 #103315Равность доказывается просто — опускаем среднюю точку на средину нижней стороны и видим четыре фигуры попарно одинаковых. Отсюда и делаем вывод — где бы тоска внутри квадрата не находилась — пара наискосок всегда составит половину
25 Июл'14 в 07:52 #103319Правильный ответ тут уже сказали )) Но ради интриги попредержим подтверждение до вечера )))
25 Июл'14 в 08:07 #103320Меня ещё в школе научили, что "видно" это не доказательство, а после того как на глаз выкопали котлован…
Я вполне допускаю, что сумма площадей противоположных четырёхугольников будет равна, но мне лень в эту сторону вырисовывать доказательство (хотя интуитивно — гдето оно так и есть).
короче, данное свойство "средней точки" мне не известно и требует дополнительных доказательств (для меня).
25 Июл'14 в 09:44 #103321это задачка я думаю чисто из темы логических решений в плоскости пропорций(наверно у школьников) смысл в том, что сколько не перемещай центр всё будет менятся пропорцианально при условии что стороны самого квадрата равны . мой ответ — 28. Десятых и сотых здесь быть не может, изначально все цифры целые. Даже можно математикой обосновать…
25 Июл'14 в 12:16 #103322Короче решил провести эксперимент
Сначало подумал обрисовать в автокаде и там бы уже она точно от меня никуда не делась) Но не тут то было! Сделал скрин, вставил, а по горизонтали картинка немного вытянута.
Тогда подумал, нафиг мне не нужна именно эта картинка. Главное чтобы доказать мои расуждения, которые впринципе подтверждены были выше другими форумчанами. А именно замерил площади фигур, прилегающих к противоположным углам. Внимание! Для проверки, эксперимент провел несколько раз перемещаяя точку внутри квадрата))) И правда суммы площадей фигур равны.
Да пусть заклюют меня математики, но если у меня мозгов на решение чего либо не хватает приходится импровезировать)
25 Июл'14 в 16:21 #103323Я уже который год рисую планировку и мебель в Sweet Home 3D. Там можно комнаты нарисовать, площадь посчитать и потом стены двигать — площадь сама будет пересчитываться. Так вот, где бы центральная точка в пределах квадрата не была, две площади наискосок всегда составляют пол площади квадрата.
26 Июл'14 в 03:27 #103324Правильный ответ — 36
а методов решения автор загадки заявляет как минимум 2.
-
АвторСообщения
- Для ответа в этой теме необходимо авторизоваться.



